December 26, 2014

mathgrrl
December 26, 2014

Polyhedral LEDs, Step 1: Mathematica

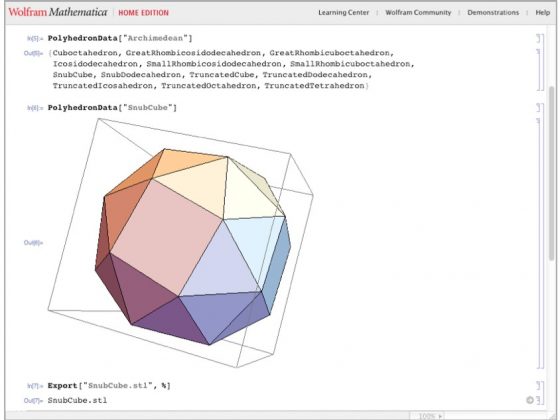
Polyhedral LEDs, Step 1: Mathematica https://mathgrrl.com/wp-content/uploads/2014/12/temp22.jpg 844 646 mathgrrl mathgrrl http://1.gravatar.com/avatar/de00911e0a27aa527aae53a60fc5b663?s=96&d=retro&r=g December 26, 2014 April 22, 2019

It’s time for another design walkthrough. This time we’ll be making polyhedral covers for LED string-lights. Since I’m just a hack at 3D design, for me the answer always involves using a chain of software programs, each of which I know how just enough about to get by, in this case Mathematica, TopMod, and Tinkercad. Each ornament is a hollowed-out instellated Archimedean solid or dual… // Hacktastic

mathgrrl
December 26, 2014

3D Printing

Holiday Belt-Tightening

Holiday Belt-Tightening https://mathgrrl.com/wp-content/uploads/2014/12/IMG_2686.jpg 640 480 mathgrrl mathgrrl http://1.gravatar.com/avatar/de00911e0a27aa527aae53a60fc5b663?s=96&d=retro&r=g December 26, 2014 April 22, 2019

Do you ever get 3D prints that look stringy or lumpy? This week we were seeing a lot of weird-looking prints from one of our Replicator 2’s, so we decided it was time for some holiday hardware maintenance. And wow, did it ever make a difference. After tightening a saggy X-axis belt we’re back as good as new. Tightening the belt isn’t difficult but it isn’t much fun either… // Hacktastic

Friday, December 26, 2014

Polyhedral LEDs, Step 1: Mathematica

Holiday Belt-Tightening