This week we created a special collection of 3D knot models based on some old projects we did with students a few years ago. To recreate these knots we used our old data to recode each of the models in a consistent way in OpenSCAD. This year’s version of the knots are scaled and sized to form a matching set suitable for printing on SLS printers like the ones at Shapeways. This means that we can have fancy, colorful Nylon Plastic versions of all our favorite knots, and even print a few in Steel.
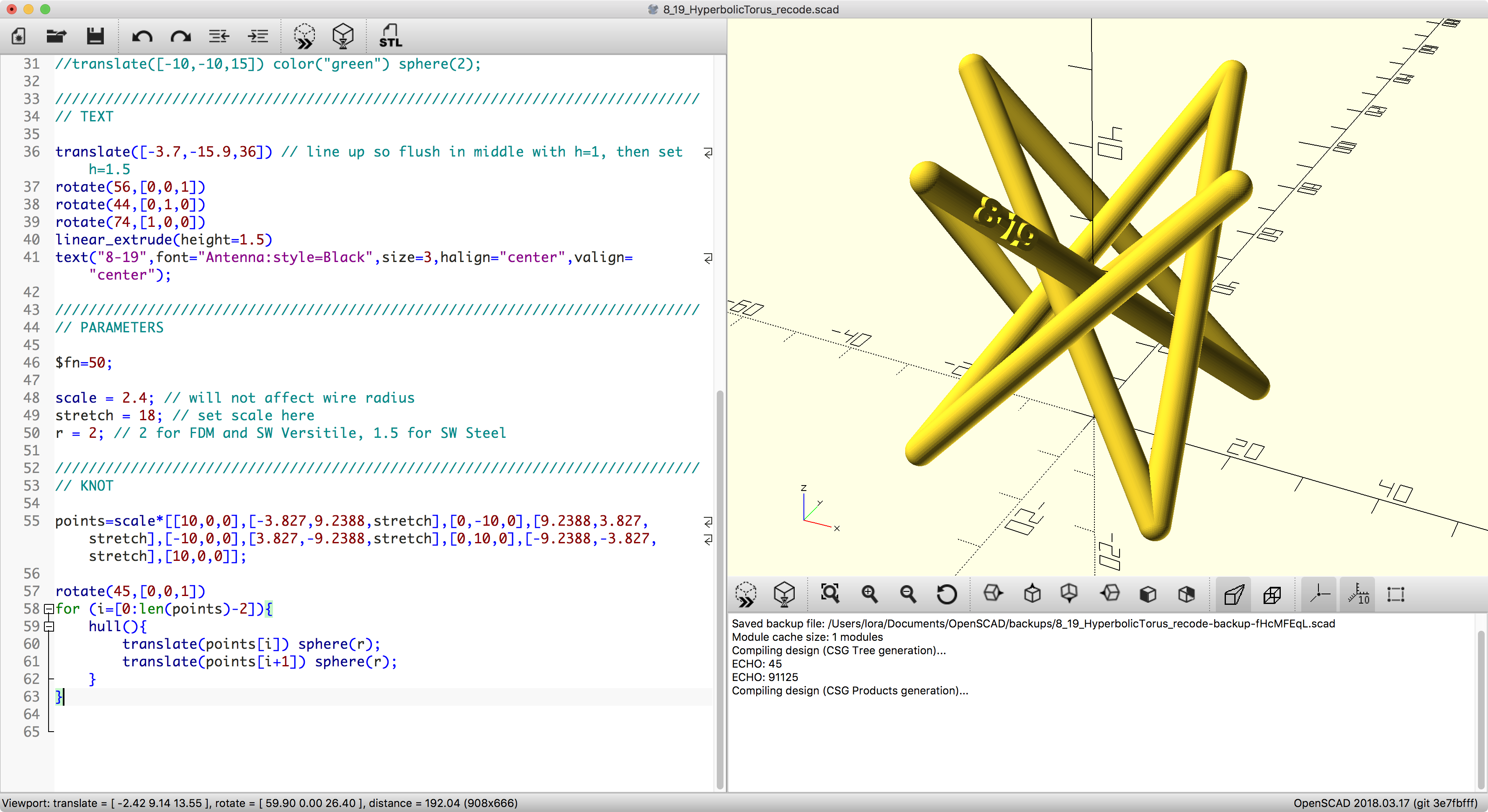
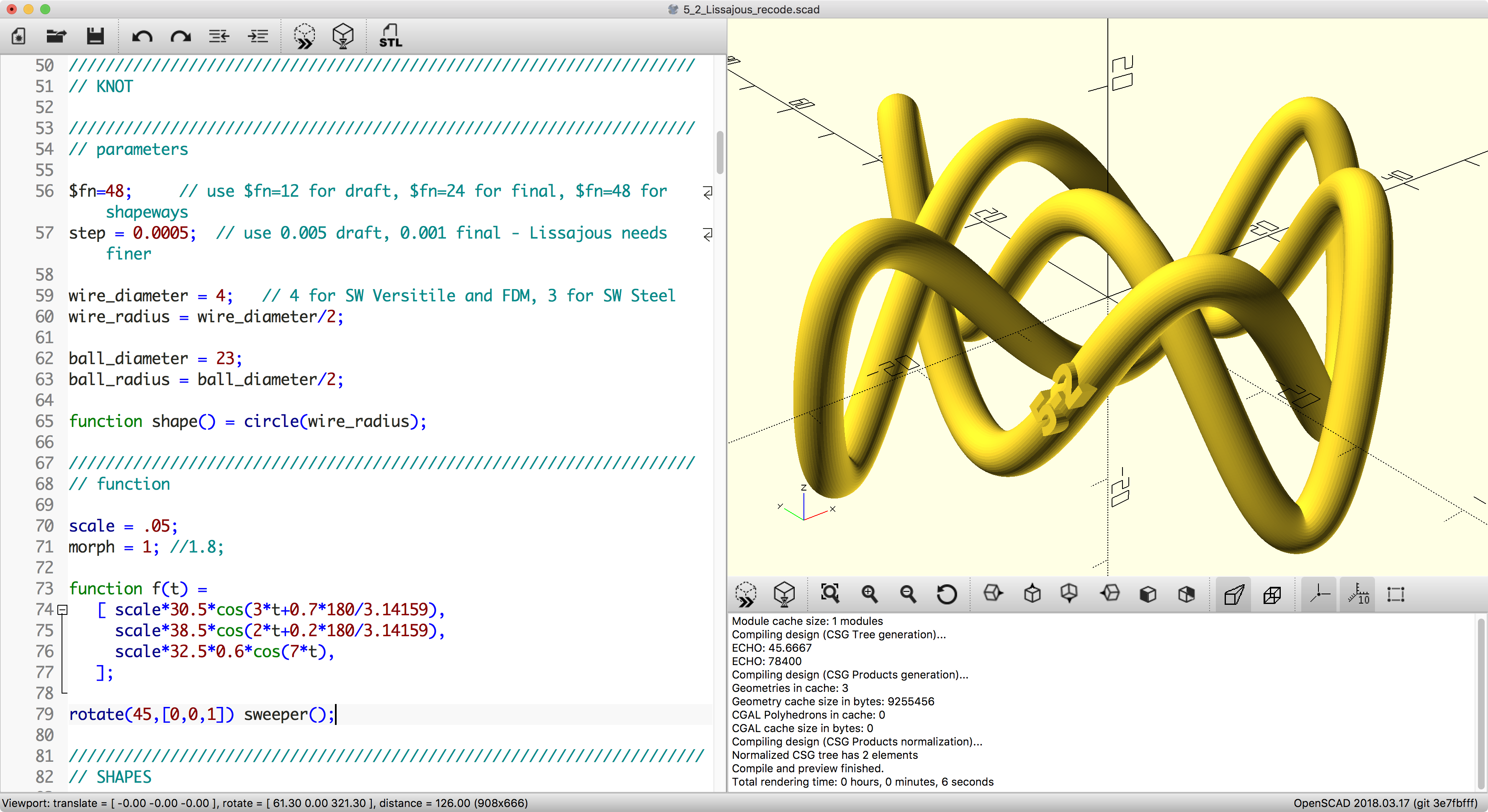
We’ll post pictures when the models return from Shapeways in a week or two, but for now here are a couple of nice renders, of a Hyperbolid Stick Knot and a Lissajous Three-Twist Knot:

OpenSCAD “Sweeper”
Knots are basically just closed curves in space, and the easiest way to create a closed curve in OpenSCAD is to “connect the dots” — that is, to create a list of points in space, place a small sphere at each of those points, and then connect each sphere to the next. If you only have a few datapoints then this method is perfectly acceptable. In the example below there are just eight points that need to be connected, so this method isn’t so bad.
This “connect-the-dots” method is simple, but with more points, as you would have if you were sampling close-together points to connect and make a curvy path in space, this way of generating a curve in space is really, really, really slow. Each pair of connected spheres costs a convex hull calculation, which is a very computationally expensive operation.
Luckily, there is a smarter way. The “sweeper” code library in OpenSCAD takes a sequence of datapoints on a curve and constructs one huge polyhedron from that data. At each point the sweeper code places a cross-sectional shape like a polygonal circle or a square, oriented in the direction of the curve. Then it connects successive cross-sections with faces, and puts the whole thing together with OpenSCAD’s polyhedron command. The code is a lot harder to follow than the method above, but for the most part you can ignore it and just put in your datapoints. Here’s what it looks like in action:
In the code above, notice that we define a function “f(t)” that parametrically describes the knot in space; the sweeper code samples points on this curve to get the data it needs to build the curvy polyhedron. You can get a copy of an OpenSCAD document with the required libraries (scad-utils and list-comprehension) for sweeper from the shared code files included with our Hello OpenSCAD primer.
The Special Knot Collection
The ten knots we decided to make for the new Special Knot Collection are the knots 3_1, 4_1, 5_1, 5_2, 6_2, 8_19, 10_161, and L6a4, as listed in the Rolfsen Knot Table. These knots are listed below, together with links to those knots on Shapeways, and links to blog posts that contain more information about each knot and why it is significant.
- Tritangentless Trefoil Knot — read more at MakerHome, Day 268
- Figure-Eight Stick Knot — read more at MakerHome, Day 269
- Cinqefoil Lattice Knot — read more at MakerHome, Day 272
- Lissajous Three-Twist Knot — read more at MakerHome, Day 273
- Miller Petal Knot — read more at MakerHome, Day 276
- Torus Knot (7,2) and equivalent Torus Knot (2,7) — read more at MakerHome, Day 286
- Hyperbolid Stick Knot — read more at MakerHome, Day 67
- Midway Perko Knot — read more at Hacktastic, Giant Spiky Perko Knot
- Borromean Rings –read more at MakerHome, Day 178
If you want to learn about mathematical knot theory, two great introductory books are The Knot Book by Colin Adams and An Interactive Introduction to Knot Theory by Inga Johnson and Allison K. Henrich. If there’s a special knot you’d like to see us add to our collection, please let us know!
——————
As an Amazon Associate we earn from qualifying purchases, so if you’ve got something you need to pick up anyway, going to Amazon through this link will help us keep Hacktastic running. Thanks! :)



I’d love to use this stuff but the shapes.scad module seems to be missing from the current scad-utils so its not possible to run any of the codes. Any help much appreciated.