Today I had the pleasure of meeting the 2014 USA Mathematical Olympiad champions at their awards celebration at the headquarters of the Mathematical Association of America in DC. We kicked off the day with a 3D-printing workshop. The students worked in four teams to design objects that would be printed later in the day. Most of the students had no design experience at all, but in under an hour they had collaborated to design some great things:
Three of the four models were made in Tinkercad. The spheres and half-spheres were made while the students learned how to use the Align and Hole tools. The figures with arms in the air were designed with extensive use of the Ruler tool and hand-calculated distances. The rockets were a minor miracle, as the students had decided to make one rocket that fits inside another and had to make a good guess for the amount of clearance/tolerance. They only had one try to make that guess, but they hit it square on the nose! The small rocket clicks into the large rocket beautifully.
The twisted square pyramid was made in OpenSCAD by a group in which one student had done some preliminary work (see Day 279). After a back-of-the-napkin calculation and some fights with compiling errors, this is what they made:
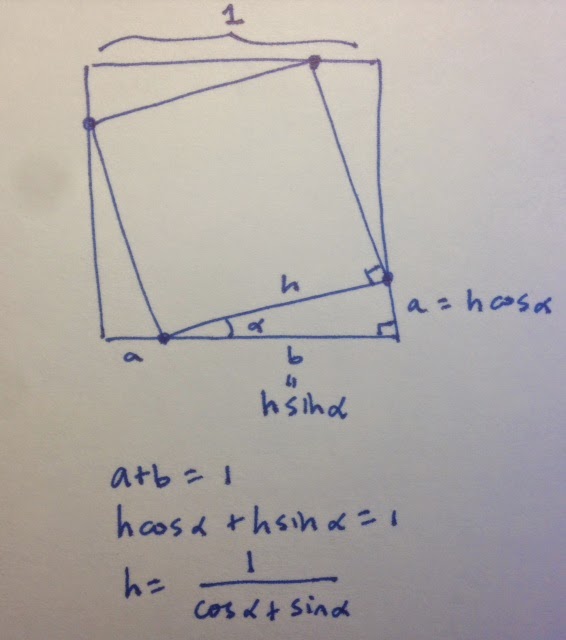
At the time I was helping all four groups and so didn’t have a chance to ask the students about their construction, so let’s take a moment to deconstruct it now. Their model is clearly a stack of rotated squares, each higher than the other and with corners on the edges of the supporting square. The part that needs calculating is determining how much to scale each square so that its corners align with the square below. From the students’ code we can see that they are using a scaling factor sc determined by the ratio of the sum of the cosine and the sine of the angle of rotation. Why did they do that? Using some basic trigonometry we can draw out the following:
Once the picture is drawn there isn’t much to do; the only thing you have to start with is the angle alpha and the original side length of 1. With a little trigonometry you can figure out the lengths of the legs a and b in the diagram, but what you really want it is the new side length h. The key insight is to realize that a + b = 1 so that you can solve for h, which becomes the scaling factor.
The USAMO students are some of the smartest, quickest math students in the nation. The top scorers will go on to represent our country in the International Mathematical Olympiad. They will go to college pretty much wherever they want to. They’ve worked amazingly hard to get to the level they are at, including taking extra courses and training workshops from organizations like the Art of Problem Solving. When they see a problem to solve they dive in fearlessly. They are curious, relentless, driven. Obsessive, even. In other words, they already think like mathematicians. Most importantly, like all mathematicians, they are experts in something that most people are terrible at, and it’s not what you think it is; it’s not calculating, or reasoning, or number sense, although they probably have all that as well. It’s being able to be WRONG. To fail. To be stuck, confused, and lost. And then to get back up again and find another way around the problem.
One reason I was particularly excited to run a 3D-printing workshop with the USAMO champions was because I knew that most of them would have tons of mathematical experience, but no experience at all with 3D printing or design. These students are used to being the best. Not the best in their class or the best in their school, or even the best in their state. The best in the country. And competing with the best in the world. They are used to success. But in a 3D-printing workshop the playing field is level again, and the USAMO students struggled with basic alignment issues, design problems, and coding syntax just like all my other 3D students do.
Sometimes in my job as a math professor I see students who were rock stars in high school burn out once they get to college and are faced with new mathematics that they don’t already know how to do. Those students somehow go from being experts at failing and problem-solving to being unable or unwilling to be stuck or feel stupid. The USAMO champions are at the top of their game and I wanted to remind them that they can still try new things and fail when they have to. And they did a great job of it. :)
UPDATE: Katherine Merow wrote a nice article for the MAA News about this called USAMO Winners Celebrated – and Challenged.



Leave a Reply