Also published at Ultimaker Education
—–
The UnKnot Conference at Denison University welcomed both mathematicians and students to a four-day celebration and exploration of mathematical knots. Knot theory is a relatively new mathematical research area, and one that is particularly suitable for mentoring undergraduate research projects; its underlying concepts are accessible and there are still many new ideas to explore. The basic idea is to think about tying a string into some kind of knot and then gluing the ends together to trap that knot — and then to do that again to create another knot, and compare. How can you tell whether or not these two knots are really the same, in the sense that one can be morphed into the other without cutting the string? Knot theory uses algebraic, topological, geometric, and analytic arguments to answer such questions in a more abstract sense. For a quick introduction check out this excellent Numberphile video featuring Carlo H. Séquin:
The conference takes place at Denison University and is organized by the mathematicians Lew Ludwig of Denison and Colin Adams of Williams College. Colin is the author of the Knot Book, and Lew is a leader in early adoption of 3D printing in liberal arts colleges. Lew and artist Chris Faur ran a 3D printing seminar course last spring and you can read about all of the student projects at their class blog, 3D Printing at Denison.
At this year’s UnKnot conference, Lew and Chris set up two of the 3D printers from their lab for participants to observe and use: one Ultimaker 2 Extended+ filament printer and one Formlabs 2 resin printer. At the start of the conference, each machine printed giveaway knots for participants.

3D-printed Conformations of Knots through 7 Crossings
Chris even set up a UV-light drying station with a solar rotating stand inside, for curing the printed Formlabs knots. You can see a tutorial on how to build your own UV curing box on the Formlabs website.

UV curing box
Here’s what that knot looked like when it came out of the curing box (and before supports were removed):

Model with support
Next to the printers was a hands-on exhibit of 3D-printed mathematical models from Lew Ludwig, Elizabeth Denne, and the author of this article.

Tiles for making mosaic knots and links, by Lew Ludwig

3D-printed Mathematical models by Elizabeth Denne (dennedesigns) and Laura Taalman (mathgrrl)
The first night of UnKnot ended with a 3D printing workshop introducing Tinkercad, Mathematica, and OpenSCAD as tools for designing and exporting 3D-printable knot models. Over the next three days, the 100 faculty and student participants presented and attended a wide array of talks about mathematical knot theory research.

In their spare time, some of them also created 3D-printable designs to support their own research and knotty interests, and printed them on the machines. For example, Sean O’Neil from the University of Texas wrote some OpenSCAD code to generate pretzel knot models:

A pretzel knot
Selina Foster and a team of students under the direction of Jennifer McLoud-Mann from the University of Washington Bothell used Tinkercad to design and then print tiles for building hexagonal mosaic knots. They are almost done with their mathematical research paper “Hexagonal Mosaic Knots” and should be putting it on the arXiv in the near future. Here are their hex tiles in the design stage and then in printed form:
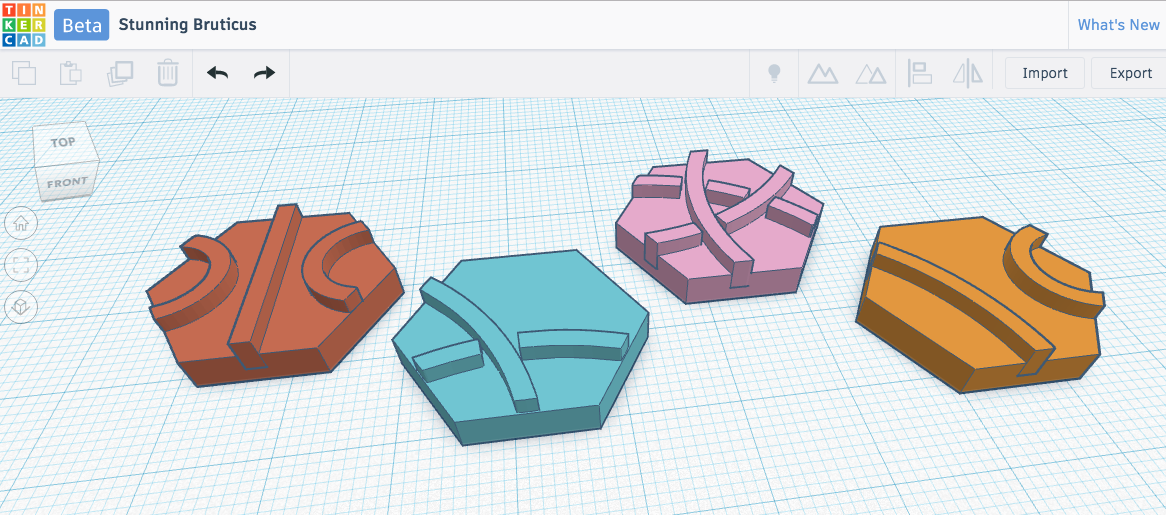
Hexagonal mosaic knots

And co-organizer Colin Adams used OpenSCAD to create a hyperboloid stick conformation of a torus knot, shown here printing, with supports removed, and in its final form:

Printing of hyperboloid stick conformation of a torus knot

Knot with support

Knot theorists are a pretty happy bunch; here we are in one big knot:

And one of the participants was particularly happy, because at the end of the conference she won a 3D printer to take home to her mathematics department! Cindy McCabe from the University of Wisconsin Stevens Point won a drawing for a brand-new Ultimaker 2+, courtesy of the community team at Ultimaker North America.

Cindy has already started printing and documenting her journey at her new 3D printing blog). Stay tuned for an article from Cindy on this blog very soon!
——————
As an Amazon Associate we earn from qualifying purchases, so if you’ve got something you need to pick up anyway, going to Amazon through this link will help us keep Hacktastic running. Thanks! :)



Leave a Reply