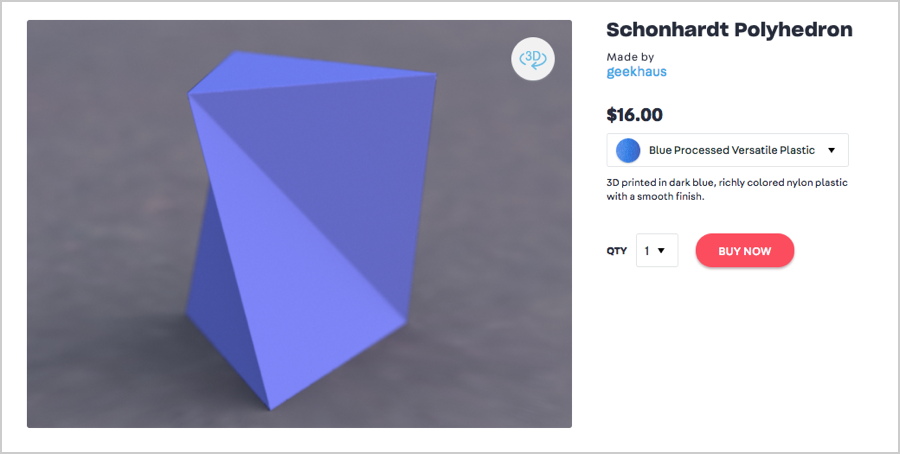
Not every polyhedron is tetrahedralizable. The simplest example is the Schönhardt polyhedron, which is a twisted triangular prism constructed in such a way that all tetrahedra that share vertices with the polyhedron fall into the exterior. This means that the Shönhardt polyhedron can’t be subdivided into tetrahedra using only its original set of vertices.
In OpenSCAD, the Schönhardt polyhedron can be constructed with just two simple lines of code, using linear_extrude and the $fn option:
linear_extrude(height=10,twist=30,slices=1)
circle(5,$fn=3);
If you’re interested in non-tetrahedralizable objects, you can see two more at the Geometry Junkyard. Or check out these great books on computational geometry:
- Discrete and Computational Geometry, Devadoss/O’Rourke
This textbook is a nice bridge between the algorithmic and theoretical. You can see the Table of Contents and all of Chapter 1 free online. - Computational Geometry, de Berg/Cheong/van Kreveld/Overmar
A more advanced textbook, and the one used in Suri’s and Ungor’s Computational Geometry courses in the list below. The Table of Contents and all of Chapter 15 are free online.
If you want to hold and examine this object in real life, then you can 3D print our free Schönhardt Polyhedron at Thingiverse:
Or, if you don’t have a 3D printer and want to order a printed copy, now you can get one at Shapeways:
——————
As an Amazon Associate we earn from qualifying purchases, so if you’ve got something you need to pick up anyway, going to Amazon through this link will help us keep Hacktastic running. Thanks! :)




Leave a Reply