Thingiverse link: http://www.thingiverse.com/thing:272833
Settings: MakerWare custom profile described in Day 194, on a Replicator 2.
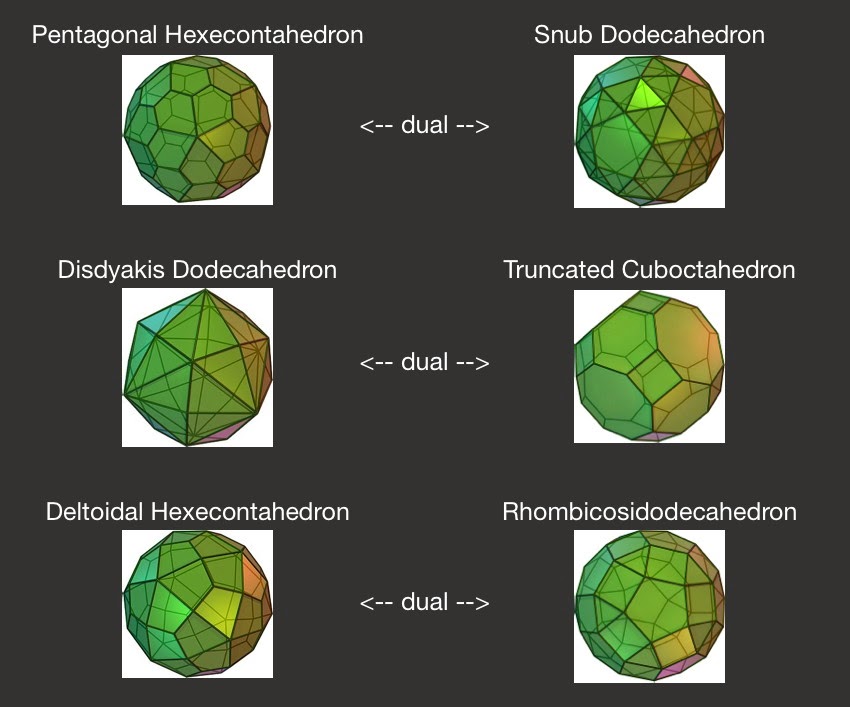
Technical notes, math flavor: Catalan solids are the polyhedra that are the duals of the Archimedean solids. To recap with some nice pictures from Wikipedia, the three Catalan solids we’ve printed (on the left) have the following Archimedean duals (on the right):
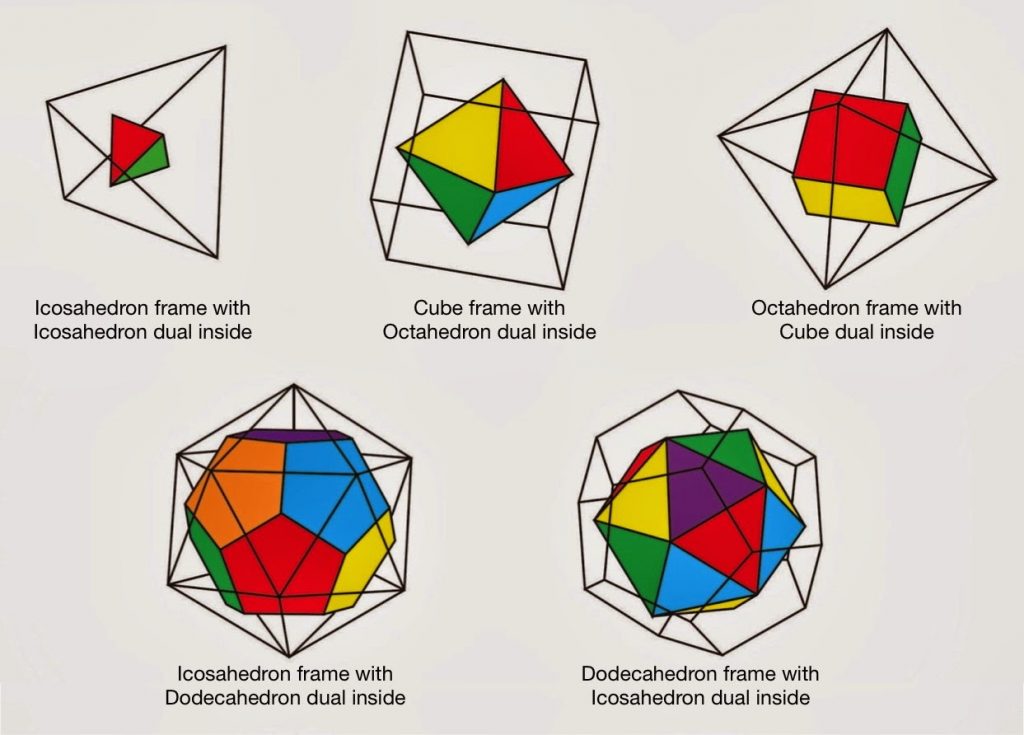
Look at these pairs of polyhedra for a minute and see if you can figure out what “dual” means. Then look at the picture below from donsteward’s blog instead, for some much easier examples. The picture below shows black wireframes of the five Platonic solids (polyhedra whose faces are all the same regular polygon and for which every vertex has the same degree) along with colorful models of their duals. In order from left to right and top to bottom: The dual of the tetrahedron is itself, the dual of the cube is the octahedron, the dual of the octahedron is the cube, the dual of the icosahedron is the dodecahedron, and the dual of the dodecahedron is the icosahedron.
From these figures it is much clearer what we mean by duality here, namely: to obtain the dual of a polyhedron we draw a vertex in the center of each face and then connect those vertices with edges. Mathematicians often say that we “replace the faces by vertices and the vertices by faces” when they want to express this concept. So, for example, each five-sided face of the dodecahedron in the last wireframe picture above corresponds to a five-degree vertex in the colorful icosahedron inside it, and each three-degree vertex in the last wireframe picture above corresponds to a three-sided face of the colorful icosahedron inside it. Now you can go back to our fancy Catalan and Archimedean solids in the first picture and see if you can spot the same pattern!





Leave a Reply