Today’s post is contributed by Chris Wallace, also known as kitwallace on Thingiverse, and author of The Wallace Line. He is the creator of the Rolling Knot, Mobius Strip, and Concave Polyhedra models on Thingiverse that have been featured here as well as the amazing Knot Server to OpenSCAD code (see Days 151, 153, 168, and 215). Thank you, kitwallace, for everything you have made possible, and for today’s post!
The open source project OpenSCAD is the programmer’s 3-D language. The language allows primitive object like cubes to be defined and combined using the Constructive Solid Geometry operations such as union, difference and intersection. Complex polyhedra can be defined in terms of points and, until the latest release, triangles. Now OpenSCAD allows faces to be used so that the programmer doesn’t have to triangulate faces. So a cube can also be made with:
points = [
[ 0.5, 0.5, 0.5],
[ 0.5, 0.5, -0.5],
[ 0.5, -0.5, 0.5],
[ 0.5, -0.5, -0.5],
[-0.5, 0.5, 0.5],
[-0.5, 0.5, -0.5],
[-0.5, -0.5, 0.5],
[-0.5, -0.5, -0.5]];
faces = [
[ 4 , 5, 1, 0],
[ 2 , 6, 4, 0],
[ 1 , 3, 2, 0],
[ 6 , 2, 3, 7],
[ 5 , 4, 6, 7],
[ 3 , 1, 5, 7]];
polyhedron(points,faces);
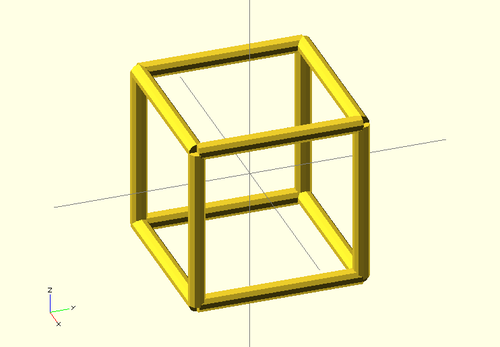
Until the latest release of OpenSCAD it hadn’t been possible to dynamically create the lists defining the polyhedra. This means that developers had to resort to quite awkward unions of primitives to build up complex objects. So one way to make a wire-fame model is to position a cylinder along each edge of each face. We can do that with a recursive module:
module make_face_edges (face,points,i=0) {
if (i < len(face)) {
assign( p1 = points[face[i]],
p2= points[face[(i + 1) % len(face)]])
union() {
locate(p1,p2)
cylinder(r=wire_radius, h = norm(p2-p1));
make_face_edges (face,points,i+1);
}
}
}
module make_faces(faces,points) {
for (i = [0:len(faces)-1])
make_face_edges(faces[i],points);
}
wire_radius=1;
scale=20;
spoints = scale * points;
make_faces(faces,spoints);
The locate(p1,p2) module changes the coordinate system so it is centered on p1 with the z-axis pointing to p2. It was originally written to create knots. It is in the form of a transform which applies to all its children.
module locate(p1, p2) {
assign(p = p2 – p1)
assign(distance = norm(p)) {
translate(p1)
rotate([0, 0, atan2(p[1], p[0])])
rotate([0, atan2(sqrt(pow(p[0], 2)+pow(p[1], 2)),p[2]), 0])
children();
}
}
However, such models prove very slow to render when there are large numbers of edges. For example, here is one of the Catalan polyhedra, the Pentagonal Icositetrahedron, formed from 20-sided cylinders:
I found a different approach in the work of Paul Draghicescu (pdragy on Thingiverse), where the object is created by forming a shell made by removing the same polyhedron scaled down from itself, then removing prisms from each face. You can see it in this see-thu model:
The latest release of OpenSCAD supports a concat() function which together with recursive functions enables lists to be computed. In the script which creates this object, we have to centre the points in a face and this means subtracting the average of the points from each of the points. Until now that operation hasn’t been possible but now we can write a recursive function:
function vsub(points,c,i=0) =
i < len(points)
? concat([points[i] – c], vsub(points,c,i+1))
: [];
Similarly we can transform every point in a list:
function transform_points(list, matrix, i = 0) =
i < len(list)
? concat([ transform(list[i], matrix) ], transform_points(list, matrix, i + 1))
: [];
where the functions vec3() and transform() are defined as:
function vec3(v) = [v.x, v.y, v.z];
function transform(v, m) = vec3([v.x, v.y, v.z, 1] * m);
This allows us to find the centre and normal to each face, transform to the xy-plane and project to a polygon, then extrude a prism and finally reposition that prism back to the original face and remove it from the shell to create a cut-way model, here of a dodecahedron:
This is much faster to render than the wire-frame model and no nasty vertexes. The amount of cutout and the thickness of the shell can be adjusted, as can the inclination of the prism which turned out be useful when creating objects with very sharp vertexes.
Later I realized that if I made the prisms pyramids, I could add them to create stellated polyhedra or ‘excavate’ with then to yield convex polyhedra such as the Great Dodecahedron and Hugels’ solid:
Powerful though OpenSCAD is, its ability to read data from external sources is limited to a few special case. Matrices can be loaded to define a surface, DXF files read to create a 2D object and STL files loaded. OpenSCAD code can be included, but the name of the file is static. Consequently scripts which can create multiple solids must include all the data needed and this makes these scripts quite complicated and less flexible.
In my search for coordinates for mathematical polyhedra, I came across David McCooey’s wonderful site providing data and Java Applet viewers for hundreds of polyhedra. Any one of them would be interesting to convert into STL for viewing and printing. In my work with web site development I use another functional language, XQuery, developed for manipulating XML data. Using this language running on the open source eXistdb native XML database, I’m developing a web site to browse over this corpus of polyhedra, extract the coordinates from the text file which is included on the site and then generate OpenSCAD code for the selected style of object. Some coordinates transformations are done by XQuery. These include changing the winding of faces from right-haded to left-handed and computing edges from faces.
I’m fond of a ‘Grook‘ (a kind of poetic aphorism) by the Danish designer and poet Piet Hein: Every problem you solve creates ten problems more. It is certainly true of this work: each time you try to solve one problem, like the construction of the regular solids, you are led into new areas of problems and faced with new difficulties. That’s the thrill of this work and the pleasure of finding others like Laura similarly solving and posing new problems, helpful people on the OpenSCAD forum and generous people like David McCooey. I’m writing up my journey in my blog both as a log of my own work and in acknowledge of the help I’ve received for others. Thank you all.
UPDATES: For updates and further information see the OpenSCAD and Polyhedra post on kitwallace’s blog The Wallace Line.








Leave a Reply