Just three knots left in the conformation series that we started on Day 266! Today we have the knot 7_5 in a tangle conformation, where you can clearly see the Conway notation [322] for this knot; note the one three-twist and two two-twists in the red model on the right:
Thingiverse link: http://www.thingiverse.com/make:82546
Settings: MakerBot Replicator 2 with our usual custom knot slicer settings.
Technical notes, KnotPlot flavor: This knot was made by JMU student Greg Houchins using KnotPlot. Here is what he has to say about his design process:
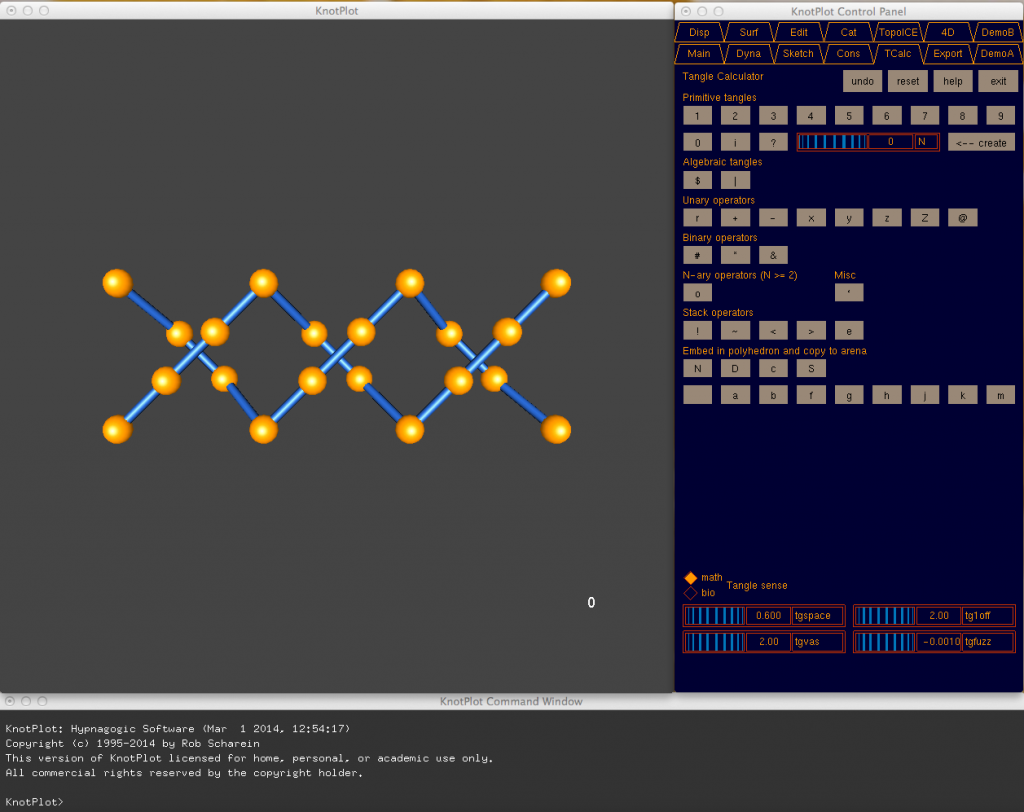
To make the 7_5 model (with Conway notation [322]), open the KnotPlot Tangle Calculator and click on the number 3 to create the tangle with 3 clockwise rations. Then transform the knot with the r button and press the number 2 button to form the tangle with two clockwise rotations. To adjoin them, press the # button. Then transform them again with the r button, make another tangle with 2 rotations, and adjoin them with #. To finalize the knot, press the N button to make the numerator knot, which is what we want. One this knot is formed, we can export it as an .obj file by going to the KnotPlot command line and typing objout 7_5knot (where “7_5knot” is the title of the file it will create).





Leave a Reply