Also published at Shapeways Magazine
—–

8 bit Mario Block by 8 bit Nirvana
Well, fun fact: I’m a math professor, so buckle up and get ready for a an in-depth look at geometry and trigonometry! Wait, don’t go… I’m just kidding; today I’m just going to give you the answers! This Tutorial Tuesday is a cheat sheet for figuring out side and angle measurements of triangles. If you care to delve deeper into the mathematics, then you can follow the video tutorial links after each table below.
When Am I Ever Going to Use This?
Ah, the age-old mathematics question. Let’s start with an example. Suppose you are making a trophy with a slanted base, and want to add text to the front of that base. You might know the lengths of the horizontal and vertical sides of the red triangle shown in the figure below, and want to know the length of the diagonal, to know how much height will be available for text. Or you might want to know the green angle shown in the figure, to know exactly how much to slant the text to align with the angled base.
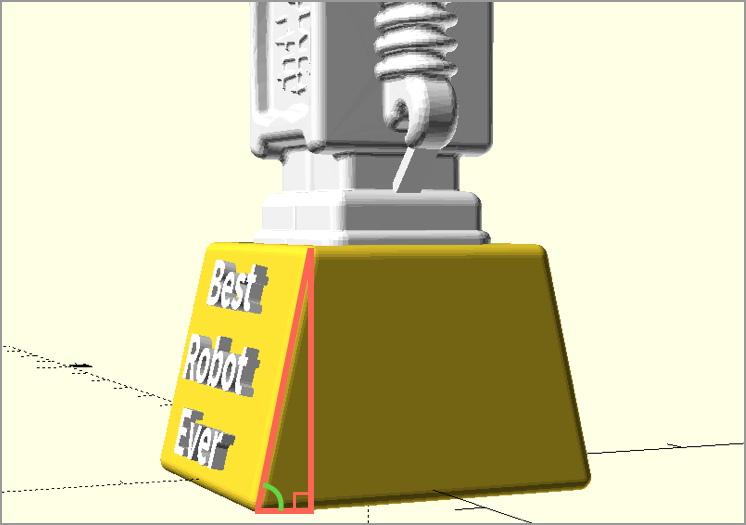
Some of the most common math questions I get from non-math designers boil down to trigonometry questions like these. In the three sections below we’ll provide quick and easy shortcuts for finding length and angle measurements of right-angle triangles.
Side From Two Sides
Let’s start simple, with something you might remember from school: If you know any two side lengths in a right triangle, then you can solve for the length of the remaining side, using the famous Pythagorean Theorem. In the figure below, suppose you know the sides A, B, and/or C, and want to find the length of the side X.

For example, in our robot trophy example, suppose the vertical leg of the triangle is A=35 mm and the horizontal leg is B=5 mm. Using the first formula in the figure above, we can find the available height for the slanted text area by typing “square root of 35^2 + 5^2” into the free online calculator and algebra system Wolfram Alpha, to get X=35.355 mm, as follows:
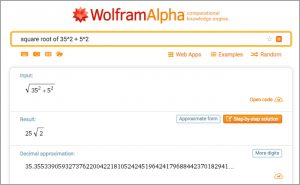
If you want to know more about the math behind these calculations, check out the Kahn Academy video Introduction to the Pythagorean Theorem.
Side From Side and Angle
If you know any one of the non-right angles in a right triangle, plus the length of any of the three sides, then you can find the length of any of the remaining sides using trigonometry, with the functions sine, cosine, and tangent. If you can’t remember how to work with those functions, or even if you’ve never heard of them before, don’t worry. You can use the buttons “sin”, “cos”, and “tan” on any calculator, or on Wolfram Alpha.
There are six situations to consider, depending on how the angle you know is situated with respect to the side length that you know, and the side length that you don’t know. For each diagram in the figure, suppose you know the labeled angle and either A, B, or C, and want to find the length of side X.
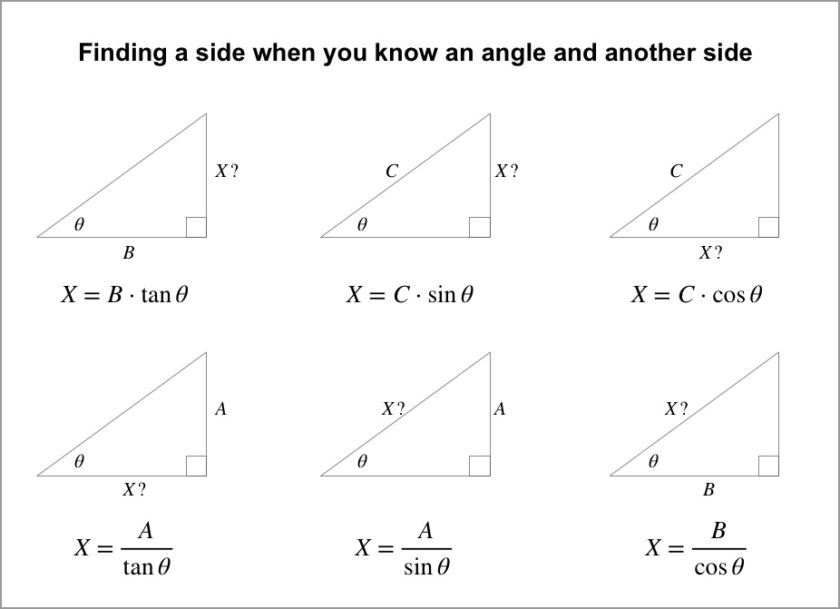
For the math behind this magic, check out the Kahn Academy’s series of videos on Trigonometry with right triangles.
Angle From Two Sides
Finally, what if you know at least two side lengths of a right triangle and want to find one or more of the non-right angles of that triangle? To do this we use the inverse trigonometric functions: inverse sine, inverse cosine, and inverse tangent. For the purposes of this cheat sheet you don’t need to learn what these functions are, except that they appear as “arcsin”, “arccos”, and “arctan” (or sometimes with notation like “sin-1“) on your calculator or Wolfram Alpha.
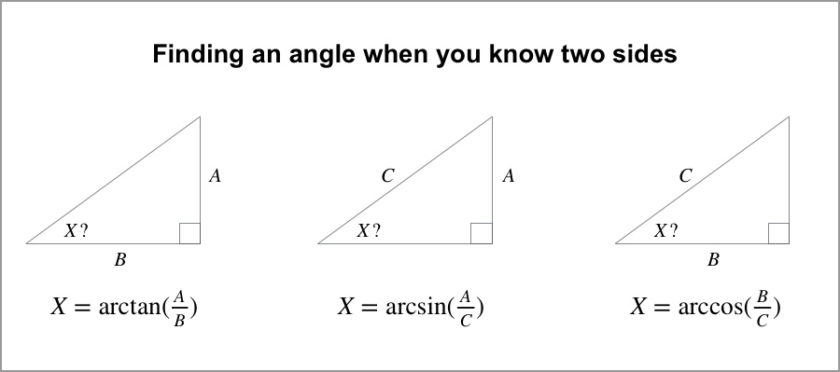
For help using inverse trigonometric functions to calculate angle measures, check out the Kahn Academy video Using inverse trig functions with a calculator. If you’re curious about the mathematics of inverse trigonometric functions, a good place to start is with the Kahn Academy video Inverse trig functions: arcsin.
Let us know if you find these cheat sheets helpful in your design work, and what you might want us to cover next! This post will follow up with a “Part 2” later that covers other design-useful mathematics such as similar triangles, the Law of Sines, and much more…
——————
As an Amazon Associate we earn from qualifying purchases, so if you’ve got something you need to pick up anyway, going to Amazon through this link will help us keep Hacktastic running. Thanks! :)




Leave a Reply