Publications
Research Papers

Modeling Dynamical Systems for 3D Printing
Stephen Lucas, Evelyn Sander, and Laura Taalman
Notices of the American Mathematical Society, Vol. 67, No. 11, p. 1692-1705, 2020
Full Text PDF
Abstract: In many cases, it is possible to use a black box differential equations solver to create printable models of dynamical systems such as chaotic attractors. However, sometimes a black box method is inadequate. We have therefore developed a mixed curvature method to make 3D printing possible in these cases. This mixed curvature methoduses a combination of Matlab and the cost-free software OpenSCAD, designed specifically for 3D mesh export. We mostly restrict our discussion to solutions of differential equations, but we end with an extention to the context of more general dynamical structures for iterated maps and ordinary and partial differential equations.

Wallpaper Patterns for Lattice Designs
Laura Taalman and Carolyn Yackel
Proceedings of Bridges 2020: Mathematics, Art, Music, Education, Culture, pages 223-230, 2020.
Full Text PDF
Abstract: Mathematicians have established that there are exactly seventeen plane symmetry groups, known as “wallpaper patterns.” Multiple mathematical fiber arts papers describe subsets of those patterns that are suitable for textile design with grid-based media such as knitting and cross-stitch. This paper extends the existing library of these patterns to include orientation-based variations and four-fold rotations. In particular we enumerate all plane lattice symmetries that can be generated from square tiles using lattice translations and combinations of other lattice symmetries. This work has application beyond mathematics as we also provide a useful patterning tool for knitting and fiber arts designers; we introduce Symmetry Generator software created using Python/Processing and OpenSCAD which provides a method for exporting plane lattice symmetry designs as hand knitting patterns or as physical punch cards for use in knitting machines.

Optimizing Morton’s Tritangentless Knots for Rolling
Abigail Eget, Stephen Lucas, and Laura Taalman
Proceedings of Bridges 2020: Mathematics, Art, Music, Education, Culture, pages 367-370, 2020.
Full Text PDF
Abstract: Tritangentless knots have a curious and beautiful property: when realized as physical 3D printed models, they roll. Some tritangentless parameterizations roll more easily and freely than others. In this paper we numerically optimize parameters to obtain the most “aesthetically pleasing” rolling knots and then create physical models of these knots using 3D printing, thereby leveraging mathematical tools to obtain an elegant kinetic sculpture.
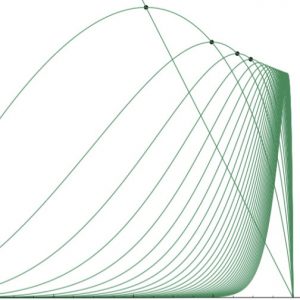
Opportunity costs in the game of best choice
Brant Jones, Laura Taalman, and students Madeline Crews, Kaitlyn Myers, Michael Urbanski, and Breeann Wilson
Electronic Journal of Combinatorics, Volume 26, Issue #1, 2019
Full Text PDF
Abstract: The game of best choice is a model for sequential decision making with many variations in the literature. Notably, the classical setup assumes that the sequence of candidate rankings are uniformly distributed in time and that there is no expense associated with conducting the candidate interviews. Here, we weight each ranking permutation according to the position of the best candidate in order to model costs incurred from interviews for candidates that are ultimately not hired. We compare our weighted model with the classical model via a limiting process. It turns out that imposing even infinitesimal costs on the interviews results in a probability of success that is about 28%, as opposed to 1/e ≈ 37% in the classical case.
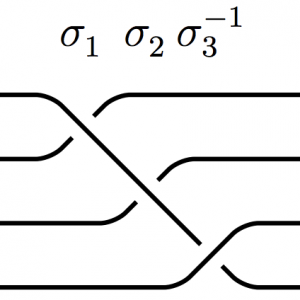
Sequences of Spiral Knot Determinants
Laura Taalman, with students Ryan Stees and Charlie Kim
Journal of Integer Sequences, Vol. 19, Issue #1, 2016
Full Text PDF / MathSciNet Review / Citations
Abstract: Spiral knots are a generalization of the well-known class of torus knots indexed by strand number and base word repetition. By fixing the strand number and varying the repetition index we obtain integer sequences of spiral knot determinants. In this paper we examine such sequences for spiral knots of up to four strands using a new periodic crossing matrix method. Surprisingly, the resulting sequences vary widely in character and, even more surprisingly, nearly every one of them is a known integer sequence in the Online Encyclopedia of Integer Sequences. We also develop a general form for these sequences in terms of recurrence relations that exhibits a pattern which is potentially generalizable to all spiral knots.
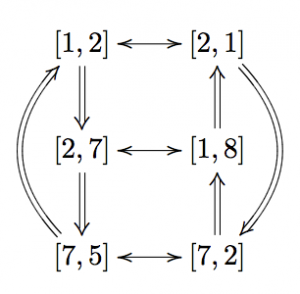
Nest graphs and minimal complete symmetry groups for magic Sudoku variants
Beth Arnold, Rebecca Field, John Lorch, Stephen Lucas, and Laura Taalman
Rocky Mountain J. Math, Vol. 45, no.3, 2015
Full Text PDF / MathSciNet Review / Citations
Abstract: We identify modular-magic Sudoku boards that can serve as representatives for equivalence classes defined from the modular-magic physical symmetries. This will allow us to identify a restricted set of relabeling symmetries that, together with the physical symmetries, forms a minimal complete modular-magic Sudoku symmetry group. We conclude with a simple computation that proves the non-obvious fact that the full Sudoku symmetry group is, in fact, already minimal and complete.

Heartless Poker
Dominic Lanphier and Laura Taalman
MOVES: Research in Recreational Math, Princeton University Press, 2015
Full Text PDF
Abstract: The probabilities, and hence the rankings, of the standard poker hands are well-known. We study what happens to the rankings in a game where a deck is used with a suit missing, or with an extra suit, or extra face cards. In particular, does it ever happen that two or more hands will be equally likely? In this paper we examine this and other questions, and show how probability, some analysis, and even number theory can be applied.

Solitaire Mancala games and the Chinese Remainder Theorem
Brant Jones, Laura Taalman, and Anthony Tongen
American Mathematical Monthly, Vol.120, No. 8, 2013
Full Text PDF / Citations
Abstract: Mancala is a generic name for a family of sowing games that are popular all over the world. There are many two-player mancala games in which a player may move again if their move ends in their own store. In this work, we study a simple solitaire mancala game called Tchoukaillon that facilitates the analysis of “sweep” moves, in which all of the stones on a portion of the board can be collected into the store. We include a self-contained account of prior research on Tchoukaillon, as well as a new description of all winning Tchoukaillon boards with a given length. We also prove an analogue of the Chinese Remainder Theorem for Tchoukaillon boards, and give an algorithm to reconstruct a complete winning Tchoukaillon board from partial information. Finally, we propose a graph-theoretic generalization of Tchoukaillon for further study.

Mancala Matrices
Laura Taalman, Anthony Tongen, and students Ben Warren, Fanya Wyrick-Flax, and Iris Yoon
College Math Journal, Vol. 44, No. 4, September 2013
Full Text PDF / MathSciNet Review / Citations
Abstract: We introduce a new matrix tool for the sowing game Tchoukaillon that enables us to non-iteratively construct an explicit bijection between board vectors and move vectors. This allows us to provide much simpler proofs than currently appear in the literature for two key theorems, as well as a non-iterative method for constructing move vectors. We also explore extensions of our results to Tchoukaillon variants that involve wrapping and chaining.
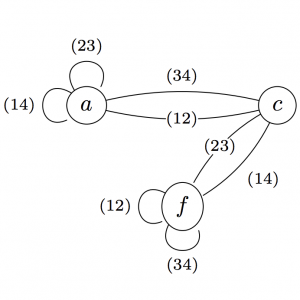
Minimal complete Shidoku symmetry groups
Beth Arnold, Rebecca Field, Stephen Lucas, and Laura Taalman
Journal of Combinatorial Mathematics and Combinatorial Computing, Vol. 87, Nov. 2013
Full Text PDF / Citations
Abstract: Calculations of the number of equivalence classes of Sudoku boards has to this point been done only with the aid of a computer, in part because of the unnecessarily large symmetry group used to form the classes. In particular, the relationship between relabeling symmetries and positional symmetries such as row/column swaps is complicated. In this paper we focus first on the smaller Shidoku case and show first by computation and then by using connectivity properties of simple graphs that the usual symmetry group can in fact be reduced to various minimal subgroups that induce the same action. This is the first step in finding a similar reduction in the larger Sudoku case and for other variants of Sudoku.
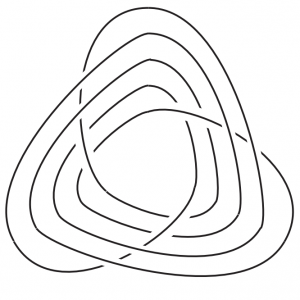
Spiral Knots
Laura Taalman, Len Van Wyk, and students Brothers, Evans, Witczak, and Yarnall
Missouri Journal of Mathematical Sciences, Vol. 22, Issue #1, 2010
Full Text PDF / Citations
Abstract: Spiral knots are a generalization of torus knots we define by a certain periodic closed braid representation. For spiral knots with prime power period, we calculate their genus, bound their crossing number, and bound their m-alternating excess.

Grobner basis representations of Sudoku
Beth Arnold, Stephen Lucas, and Laura Taalman
College Math Journal, Vol. 41, No. 2, March 2010
Full Text PDF / Citations
Abstract: This paper uses Gröbner bases to explore the inherent structure of Sudoku puzzles and boards. In particular, we develop three different ways of representing the constraints of Sudoku puzzles with a system of polynomial equations. In one case, we explicitly show how a Gröbner basis can be used to obtain a more meaningful representation of the constraints. Gröbner basis representations can be used to find puzzle solutions or count numbers of boards.
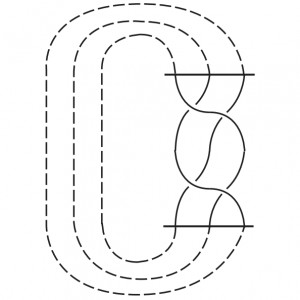
p-Coloring classes of torus knots
Laura Taalman and students Anna-Lisa Breiland and Layla Oesper
Missouri Journal of Mathematical Sciences, Vol. 21, Issue #2, 2009
Full Text PDF / Citations
Abstract: We classify by elementary methods the p-colorability of torus knots, and prove that every p-colorable torus knot has exactly one nontrivial p-coloring class. As a consequence, we note that the two-fold branched cyclic cover of a torus knot complement has cyclic first homology group.
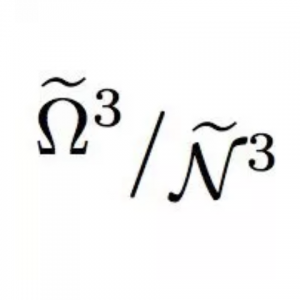
An exact sequence of weighted Nash complexes
Laura Taalman
Illinois Journal of Mathematics, Volume 52, Number 2, Summer 2008
Full Text PDF / MathSciNet Review / Citations
Abstract: Given a three-dimensional complex algebraic variety with isolated singular point and a sufficiently fine complete resolution of the singularity, we construct an exact sequence of weighted Nash complexes. We use genericity and a theorem from Hironaka to make a careful choice of transverse hyperplane that will define the maps of our exact sequence, and use the properties of the monomial generators of the Nash sheaf to construct a local basis for a certain sheaf of logarithmic 1-forms.
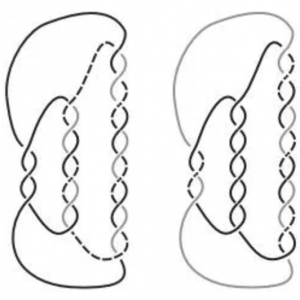
Counting m-coloring classes of knots and links
Laura Taalman and students Kathryn Brownell and Kaitlyn O’Neil
Pi Mu Epsilon Journal, Volume 12, Number 5, Fall 2006
Full Text PDF / Citations
Abstract: Two Fox m-colorings of a knot or link K are said to be equivalent if they differ only by a permutation of colors. The set of equivalence classes of m-colorings under this relation is the set Cm(K) of Fox m-coloring classes of K. We develop a combinatorical formula for |Cm(K)| for any knot or link K that depends only on the m-nullity of K. As a practical application, we determine the m-nullity, and therefore the value of |Cm(P(p,q,r))|, for any any (p, q, r) pretzel link P(p,q,r).
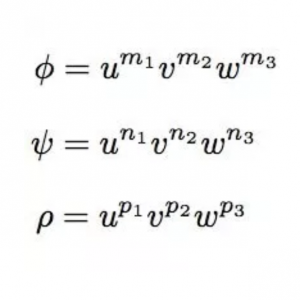
The Nash sheaf of a complete resolution
Laura Taalman
Manuscripta Mathematica 106, no. 2, 249-270, 2001
Full Text PDF / MathSciNet Review / Citations
Abstract: Every three-dimensional complex algebraic variety with isolated singular point has a resolution factoring through the Nash blowup and the blowup of the maximal ideal over which the second Fitting ideal sheaf is locally principal. In such resolutions one can construct Hsiang-Pati coordinates and thus obtain generators for the Nash sheaf that are the differentials of monomial functions. The results here provide a generalization of the results of Pardon and Stern to the three-dimensional case, as well as a more conceptual view of Pati’s three-dimensional results.
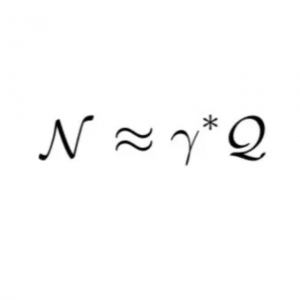
Monomial generators for the Nash sheaf of a complete resolution
Laura Taalman
Ph.D. Thesis, Duke University
Full Text PDF / Citations
Abstract: Given a complex algebraic 3-dimensional variety with isolated singular point, we show that there exists a resolution over which the generators of the Nash sheaf can be written locally as the differentials of certain monomial functions. The exponents of these monomials define a sequence of three divisors (the “resolution data”) supported on the exceptional divisor of the resolution. Using these divisors we construct an exact sequence that relates the Nash sheaf to the resolution data. As an application, we use this exact sequence to calculate certain Chern classes of the Nash sheaf, and thus Mather-Chern classes of the variety.
Articles

Parametric OpenSCAD Designs for Exploring Sierpinski-Like Carpet Fractals and Infinite Geometric Series
Laura Taalman
Construct3D, Conference Proceedings, October 2018
Full Text PDF
Abstract: Traditional uses for 3D design and printing often center around the creation of useful printed objects that serve as prototypes or final products intended for solving physical real-world problems. In this application of 3D design we are focused instead on the understanding of abstract mathematical concepts through design creation and exploration. In this paper we will introduce a specific parametric model that can be used in a mathematical liberal arts course to introduce high-level mathematical concepts such as fractals and infinite series to students with limited mathematical backgrounds.

Book Reviews: Visualizing Mathematics with 3D Printing… and Pasta by Design
Laura Taalman
The American Mathematical Monthly, Volume 125, Issue 4, March 2018
Full Text PDF
Excerpt: In Hype Cycle terminology, three-dimensional printing is now past the “Peak of Inflated Expectations,” where those new to the concept imagine that 3D printers are magical replicating microwaves that produce just about anything you want, quickly and easily, with the push of a button. Most of us in the mathematical community are already aware that 3D printing is not so fast, easy, or capable. Designing mathematical files for 3D printing can be difficult, frustrating, and full of dead ends. In terms of the Hype Cycle, 3D printing is solidly in what is known as the “Trough of Disillusionment” phase. The next step in the Hype Cycle is to try climb the “Slope of Enlightenment.” Part of climbing that slope is being able to see what is possible at the summit, and that is where Henry Segerman’s book comes in…
Get Henry Segerman’s book Visualizing Mathematics with 3D Printing on Amazon
Get George Legendre’s book Pasta by Design on Amazon
The Mathematics Behind xkcd: A conversation with Randall Munroe
Laura Taalman
Math Horizons, September 2012
Full Text PDF
Description: The creator of the popular web comic xkcd muses about the merits of pen and paper versus computer coding, tic-tac-toe, and where he sits on the scale of intellectual purity. This past April, Math Horizons sat down with Randall Munroe, the author of the popular webcomic xkcd, to talk about some of his most mathematical comics. We met at Christopher Newport University, Randall’s alma mater, where he was about to give an invited talk to a packed auditorium of fans.
Get Randall Munroe’s books on Amazon
Taking Sudoku Seriously
Laura Taalman
Math Horizons, September 2007
Full Text PDF / Citations
Introduction: You’ve seen them played in coffee shops, on planes, and maybe even in the back of the room during class. These days it seems that everyone is filling in gerechte designs of order 9 with square subregions. But is it math?

Puzzling Over Sudoku
Laura Taalman
Madison Magazine, September 2007
Full Text PDF
Introduction: America has been taken over by little 9 by 9 grids full of numbers. Sudoku puzzles are now a regular feature in almost every newspaper, and bookstores devote entire sections to Sudoku books. But, we’re late to the party; Sudoku has been popular since the ’80s in Japan after its first appearance in print in an American puzzle magazine in 1979.

Simplicity is Not Simple: Tessellations and Modular Architecture
Eugenie Hunsicker and Laura Taalman
Math Horizons, cover article September 2002
Full Text PDF / Citations
Description: In this article, we’ll introduce you to Gregg Fleishman’s work, modular architecture more generally, and talk about how various architectural considerations can be described in mathematical terms. Along the way, we’ll discuss and prove some basic facts about polyhedra and tessellations.
Textbooks

Taalman/Kohn Calculus
Laura Taalman and Peter Kohn
Freeman/Macmillan, First Edition 2013
Get this book on Amazon
Publisher Notes: Taalman and Kohn’s Calculus offers a streamlined, structured exposition of calculus that combines the clarity of classic textbooks with a modern perspective on concepts, skills, applications, and theory. Its sleek, uncluttered design eliminates sidebars, historical biographies, and asides to keep students focused on what’s most important—the foundational concepts of calculus that are so important to their future academic and professional careers.

Taalman Calculus with Integrated Precalculus
Laura Taalman
Freeman/Macmillan, First Edition 2013
Get this book on Amazon
Publisher Notes: Taalman’s Calculus I with Integrated Precalculus helps students with weak mathematical backgrounds be successful in the calculus sequence, without retaking a precalculus course. Taalman’s innovative text is the only book to interweave calculus with precalculus and algebra in a manner suitable for math and science majors— not a rehashing or just-in-time review of precalculus and algebra, but rather a new approach that uses a calculus-level toolbox to examine the structure and behavior of algebraic and transcendental functions.

Taalman Integrated Calculus
Laura Taalman
Houghton Mifflin, First Edition 2004
Get this book on Amazon
Textbook Excellence Award 2006, Text and Academic Authors Association
Publisher Notes: The only text on the market that truly integrates calculus with precalculus and algebra in a two-semester course appropriate for math and science majors, Integrated Calculus uses a student-friendly approach without sacrificing rigor. Students learn about logic and proofs early in the text then apply these skills throughout the course to different types of functions.This combined approach allows students to eliminate a pure precalculus course and focus on calculus, with a “point-of-use” presentation of necessary algebra and precalculus concepts.
Trade Books

Taking Sudoku Seriously
Jason Rosenhouse and Laura Taalman
Oxford University Press, 2012
Get this book on Amazon
PROSE Award for Popular Science and Mathematics 2012, Association of American Publishers
MathSciNet Review / Citations
Wall Street Journal Review by Keith Devlin
The Guardian Review by GrrlScientist
Mathematical Association of America Review by Mark Hunacek
Royal Statistical Society Review by Nicola Tilt
Mathematical Gazette Review by David Bevan
Additional reviews by Tanya Khovanova, Mike James, and Michael Lugo
Publisher Notes: Packed with more than a hundred color illustrations and a wide variety of puzzles and brainteasers, Taking Sudoku Seriously uses this popular craze as the starting point for a fun-filled introduction to higher mathematics. How many Sudoku solution squares are there? What shapes other than three-by-three blocks can serve as acceptable Sudoku regions? What is the fewest number of starting clues a sound Sudoku puzzle can have? Does solving Sudoku require mathematics? Jason Rosenhouse and Laura Taalman show that answering these questions opens the door to a wealth of interesting mathematics. Indeed, they show that Sudoku puzzles and their variants are a gateway into mathematical thinking generally. A math book and a puzzle book, Taking Sudoku Seriously will change the way readers look at Sudoku and mathematics, serving both as an introduction to mathematics for puzzle fans and as an exploration of the intricacies of Sudoku for mathematics buffs.

Taking Sudoku Seriously
Jason Rosenhouse and Laura Taalman
Seidosha Press, Japanese Translation 2014
Get this book on Amazon
Publisher notes: Taking the world by storm, enjoying “Sudoku” puzzles thorough research! This book considers a variety of interesting questions for Sudoku fans to mathematicians. “Father of Sudoku,” Kaji MaOkoshi Mr. [Corporation Nikoli President] recommends!! The authors Jason Rosenhouse and Laura Taalman understand the fun of the Sudoku boom, and in this new and interesting this book, analyze Sudoku variations from the side of mathematical research. All color. Includes over 90 original puzzles.

Taking Sudoku Seriously
Jason Rosenhouse and Laura Taalman
Machinery Industry Press, Chinese Translation 2014
Get this book on Amazon
Publisher notes: Through more than one hundred color pictures and a wealth of Sudoku, Magic Square and Sudoku Variation puzzles, this book explores higher mathematical research around the great game of Sudoku, the world’s most popular pencil puzzle. This is a math book, while at the same time, a fun puzzle book. How many Sudoku grids are there in total? How many initial clues are required for a unique solution? The authors demonstrate the fact that by answering these questions, you can open a door to a rich and interesting world of mathematics.
Puzzle Books

Rainbow Sudoku
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Puzzlewright Press, 2016
Get this book on Amazon
Publisher Notes: Who said sudoku have to be black and white? These 180 multihued puzzles come in a rainbow of glorious colors and patterns that enhance the fun. Although they begin with the standard 9×9 grid and follow the basic rules, each sudoku offers a fresh twist to tradition: perhaps every red square must contain a different number, or a puzzle may look like a jigsaw. It’s the perfect collection for solvers who enjoy a challenge that’s way out of the ordinary.

Ninecraft Sudoku
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Puzzlewright Press, 2016
Get this book on Amazon
Publisher Notes: These puzzles are not dressed to the “9’s”! That’s because not one of these sudoku contains the number 9 as a given, so solvers must do some mining to discover where they belong. Pixel-y, nerdy, creative, and challenging, Ninecraft Sudoku features nearly 190 puzzles that get harder as you go along, and includes some grids with givens that are in shapes seen in mining games.

Fifty Squares of Grey
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Puzzlewright Press, 2014
Get this book on Amazon
Publisher Notes: Whips, handcuffs . . . sudoku? When you’re in the mood for some masochistic pleasure, this variant of the popular puzzle will satisfy your desires. Each 10×10 grid is divided into ten regions of 5×2. Play like regular sudoku, except using numbers 0-9. Then comes the twist: each sudoku also has five 10-square grey regions to complete—a total of 50 squares of grey.

Double Trouble Sudoku
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Puzzlewright Press, 2014
Get this book on Amazon
Publisher Notes: This brand-new sudoku variant will have logic lovers seeing double! Instead of appearing only once in every row and column, each number appears TWICE. And instead of the usual three-by-three areas, these puzzles have irregular shapes. These twists add spice to the solving, variety to the sudoku, and make every puzzle a unique challenge for your eyes and mind.

Beyond Sudoku
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Puzzlewright Press, 2012
Get this book on Amazon
Publisher Notes: Ready to take your sudoku skills to the next level? Beyond Sudoku features more than 150 ingenious puzzles with extra regions indicated by colored squares or colored dotted lines. The play of patterns and colors makes each grid a unique work of art, and there’s only one new rule: no numbers may repeat in the extra regions. But that simple rule takes you Beyond Sudoku to a new world of challenges and fun!

No-Frills Sudoku
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Puzzlewright Press, 2011
Get this book on Amazon
Publisher Notes: Unlike many sudoku, where a third of the squares are filled in, each of these puzzles has only 18 givens (completed squares). That means fans enjoy more of a challenge. All the puzzles are expertly crafted to satisfy both casual solvers on a break and sudoku die-hards relaxing on a Sunday afternoon.

Naked Sudoku
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Puzzlewright Press, 2009
Get this book on Amazon
Publisher Notes: All the starting numbers have been stripped away, leaving you with something truly intriguing: Naked Sudoku. Each puzzle is a variation on regular sudoku, but there are no starting numbers to help. Instead, you must use other types of clues to determine where to begin. In one variant, for instance, greater-than and less-than signs point out the way. These are sudoku puzzles that will push your brain to the limit and expose your true sudoku talent.

Color Sudoku
Philip Riley and Laura Taalman, Brainfreeze Puzzles
Sterling Publishing, 2007
Get this book on Amazon
Publisher Notes: Sudoku fans will welcome this bright new twist to the popular puzzles! Every one of these ingenious creations—from “Bold X” to “Rainbow Up”—makes colors and patterns part of the solving fun. And although each puzzle maintains the normal 9×9 grid and follows the basic rules of the game, every style adds an additional restriction to intensify the challenge. In “Worms,” for example, swirly, squirmy shapes fill the grids; the numbers increase as you work your way from head to tail. “Even/Odd” features squares in two colors, depending on whether the number to fill it is even or odd. And in “Positional Board,” no two of the red squares can be the same number. They’re all lots of fun!
External Blog Posts
Shapeways Magazine, January 2017 – present
- Just in Time: Clocks!
- 3D Printing Strong and Sturdy Models
- Is your 3D model a mess? Make it printable!
- Creating Celtic Knots with Fusion 360
- Targeted Thickening with Meshmixer
- Making Meaning
- Family Design Roundup
- Design Exploration with Vectary
- Vases in Fusion 360 Two Ways: Lofting and Sculpting
- Make One Billion Snowflakes With the Snowflake Machine
- Text Wrapping with Fusion 360 Sheet Metal Tools
- Turning One Snowflake Into Billions with OpenSCAD
- Leveraging Math and Materials to Make Bangles That Fit
- Everything You Always Wanted to Know About X, But Were Afraid to Ask (Part 2)
- Here Come the Holidays
- Designing for 3D Printed Porcelain
- Candy Mold Presses With Fusion 360
- Lightning-Fast Lithophanes With Cura
- Quick Design With 3D Slash
- Custom D&D Characters With Hero Forge
- Add Custom Heraldry to Tabletop Minis With Meshmixer
- FDM=ASAP but SLS=OMG
- Thickening 3D Models With Blender
- CAD in the Cloud With Onshape
- Learn to Fly With Wings3D
- 3D Design Electronics in Tinkercad
- Repair and Prep Structure Synth Models
- Rescue 3D Models With MakePrintable
- Everything You Always Wanted to Know About X, But Were Afraid to Ask
- Design for Complexity With Structure Synth
- Oops, Now Your Photos Are TOO Good!
- Easy Pendant Creator Walkthrough
- Learn to Code in 3D With BlocksCAD
- Porcelain Topographic Models with Terrain2STL
- Full-Color Prints from Trnio Photogrammetry
- 3D Design Made Simple With Morphi
- Taking Better Photographs of Your 3D Prints
- Wrapping a Thing Around Another Thing
- Parametric Modeling With Grasshopper
- SketchUp for 3D Printed Buildings and Beyond
- Creating a Community of 3D Educators at the Construct3D Conference
- Mathematica Brings the Mathematical Bling
- First Steps with 3D Design Software Fusion 360
- Print Cheaper By Scaling… Up?
- Painting Multicolor Models in Meshmixer
- Get Some Variety With Variants
- Topological Mesh Modeling with TopMod
- Modeling for 3D Printing with Cinema 4D
- Printing the Impossible: Evolution of a Fidget Cube
- Help!
- Using Sculptris to 3D Model With Digital Clay
- What 3D Design Software Should I Use?
- No Snow? Here’s How to Make Your Own
- Making Your Designs Customizable with CustomMaker
- Quick Fixes With MeshLab
- Using OpenSCAD to Design with Code
- Beginner 3D Design With Tinkercad
- Full-Color Printing and Character Models
- Shapeways Tutorial Tuesday Kickoff!
